BrunnerCTF 2025 - Crypto challenges | MindCrafters CTF Team

Introduction

Between August 22 and 24, a very enjoyable Danish CTF took place. There were plenty of tasks, all well-balanced. It was an easier CTF, but there was a lot of fun. Currently, it has a ranking of 0, but I hope it will increase. We solved all the crypto challenges and more, but here I describe only the crypto ones. You can find more information about the CTF here. all-rev

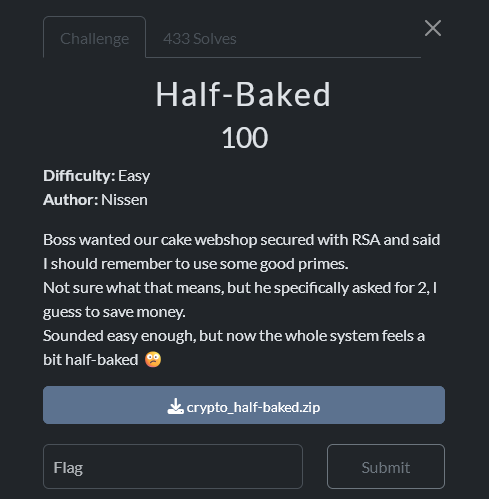
Half-backed

Writeup author: michalBB

From the file: you have n, e=65537, c. A quick observation: n is even... and even better: it turns out that v₂(n)=1337, so n = 2^1337 (no odd part!).

This is "half-baked RSA" — instead of the product of two large odd primes, the modulus is a power of two.

For n=2^k and odd e, exponentiation x ↦ x^e (mod 2^k) is a permutation on odd residues. We use the Carmichael function: λ(2^k) = 2^(k-2) for k ≥ 3.

We compute the private key: d = e^-1 mod 2^(k-2) with k=1337, so d = e^-1 mod 2^1335.

Decryption: m = c^d mod 2^1337, then convert m to bytes → you get the flag above.

Solution

# -*- coding: utf-8 -*-
# Half-baked RSA: n = 2^k, e nieparzyste → d = e^{-1} mod 2^(k-2), m = c^d mod 2^k

import re
import sys

def parse_params(path):
    txt = open(path, "r", encoding="utf-8").read()
    def grab(name):
        m = re.search(rf"{name}\s*[:=]\s*([0-9A-Fa-fx]+)", txt)
        if not m:
            raise ValueError(f"Nie znaleziono parametru: {name}")
        return int(m.group(1), 0)  # auto: 0x... lub dziesiętnie
    return grab("n"), grab("e"), grab("c")

def v2_and_oddpart(n: int):
    """Zwraca (k, odd), gdzie n = 2^k * odd i odd jest nieparzyste."""
    if n <= 0:
        raise ValueError("n musi być dodatnie")
    k = 0
    while (n & 1) == 0:
        n >>= 1
        k += 1
    return k, n  # n tu to część nieparzysta (odd)

def i2b(x: int) -> bytes:
    if x == 0:
        return b"\x00"
    length = (x.bit_length() + 7) // 8
    return x.to_bytes(length, "big")

def main():
    path = sys.argv[1] if len(sys.argv) > 1 else "half-baked.txt"
    n, e, c = parse_params(path)

    k, odd = v2_and_oddpart(n)
    if odd != 1:
        raise SystemExit(f"Ten exploit działa, gdy n jest dokładnie potęgą 2. "
                         f"Tutaj: n = 2^{k} * {odd} (odd≠1).")

    if e % 2 == 0:
        raise SystemExit("e musi być nieparzyste (inaczej brak odwrotności modulo 2^(k-2)).")

    # λ(2^k) = 2^(k-2) dla k ≥ 3
    if k < 3:
        raise SystemExit("Zbyt małe k; oczekuję k ≥ 3.")
    lam = 1 << (k - 2)

    # d = e^{-1} mod 2^(k-2)  (Python 3.8+: pow(e, -1, mod))
    try:
        d = pow(e, -1, lam)
    except ValueError as ex:
        raise SystemExit(f"Brak odwrotności e modulo 2^(k-2): {ex}")

    # Odszyfrowanie: m = c^d mod 2^k
    mod = 1 << k
    m = pow(c, d, mod)

    m_bytes = i2b(m).rstrip(b"\x00")  # często końcowe zera nie niosą informacji
    print(f"[i] k = {k}")
    print(f"[i] d = {d}")
    print(f"[i] m (hex) = {m:0x}")
    try:
        print("[i] m (ASCII) =", m_bytes.decode("utf-8"))
    except UnicodeDecodeError:
        print("[i] m (bytes) =", m_bytes)

if __name__ == "__main__":
    main()

brunner{s1ngl3_pr1m3_1s_d0ubl3_tr0ubl3}

The Complicated Recipe

Writeup author: michalBB

Solution

# -*- coding: utf-8 -*-
# S-DES decrypt of the given hex -> prints the flag

P10 = [3,5,2,7,4,10,1,9,8,6]
P8  = [6,3,7,4,8,5,10,9]
P4  = [2,4,3,1]
IP  = [2,6,3,1,4,8,5,7]
IPi = [4,1,3,5,7,2,8,6]
EP  = [4,1,2,3,2,3,4,1]

S0 = [[1,0,3,2],[3,2,1,0],[0,2,1,3],[3,1,3,2]]
S1 = [[0,1,2,3],[2,0,1,3],[3,0,1,0],[2,1,0,3]]

def perm(b, t): return [b[i-1] for i in t]
def lsh(b, n):  return b[n:]+b[:n]
def itob(x,n):  return [(x>>(n-1-i))&1 for i in range(n)]
def btoi(b):    return int(''.join(map(str,b)),2)

def kgen(k10):
    bits = itob(k10,10)
    p = perm(bits, P10); L, R = p[:5], p[5:]
    L1, R1 = lsh(L,1), lsh(R,1)
    K1 = perm(L1+R1, P8)
    L2, R2 = lsh(L1,2), lsh(R1,2)
    K2 = perm(L2+R2, P8)
    return K1, K2

def sbox(sb, b4):
    r = (b4[0]<<1)|b4[3]; c = (b4[1]<<1)|b4[2]
    return itob(sb[r][c], 2)

def F(b8, K):
    L, R = b8[:4], b8[4:]
    X = [a^b for a,b in zip(perm(R,EP), K)]
    s = sbox(S0, X[:4]) + sbox(S1, X[4:])
    p4 = perm(s, P4)
    return [l^p for l,p in zip(L,p4)] + R

def sdes_dec(byte, k10):
    K1, K2 = kgen(k10)
    x = perm(itob(byte,8), IP)
    x = F(x, K2); x = x[4:]+x[:4]   # swap
    x = F(x, K1)
    return btoi(perm(x, IPi))

hex_ct = "D1D74C5F5FDDD7ECD8B29ED8019DD801B7F2AB0128573FB2019D1C018FF2E001E7B7F2870128F28701ABF20112E0D8AB015957E79EA2"
ct = bytes.fromhex(hex_ct)

# Znany klucz z brute-force:
key = 914  # 10-bit (dec)

pt = bytes(sdes_dec(b, key) for b in ct)
print(pt.decode())

# --- Opcjonalnie: brute-force (odkomentuj, by znaleźć klucz samodzielnie) ---
# for k in range(1024):
#     p = bytes(sdes_dec(b, k) for b in ct)
#     s = None
#     try:
#         s = p.decode()
#     except UnicodeDecodeError:
#         continue
#     if "{" in s and "}" in s:
#         print("KEY:", k, "PLAINTEXT:", s)
#         break

brunner{5D35_15_N0T_H4RD_1F_Y0U_KN0W_H0W_T0_JU5T_B4K3}

The Cryptographic Kitchen!

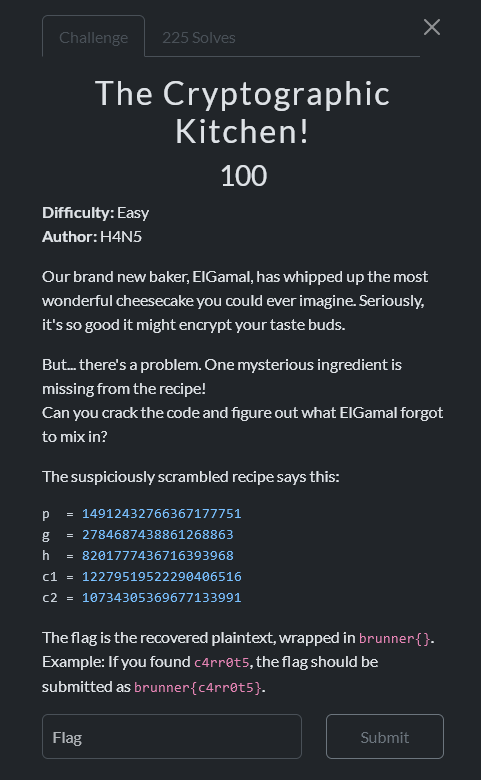
Writeup author: michalBB

We have ElGamal in $\mathbb{Z}_p^*: c_1 = g^k$ , $c_2 = m \cdot h^k$ . The order of $g$ is $125 \cdot q$ , where $q = 25934665686063857$ .

Pohlig–Hellman in the subgroup of order $125$ gave: $k = 19 \pmod{125}$ . In the subgroup of order $q$ (using $g^{125}$ , $c_1^{125}$ ). I used Pollard Rho for DLP and got: $k = 227993451121983 \pmod{q}$ . Assembled via $CRT ⇒ k = 319224381329769394$ .

Decryption:

$m = c_2 \cdot (h^k)^{-1} \mod p = 108256065500018$

which interpreted as ASCII bytes gives buTT3r.

brunner{buTT3r}

Cheesecake

Writeup author: michalBB

The script for the final challenge verifies that MD2(mix) equals 8350e5a3e24c153df2275c9f80692773 (which is the MD2 hash of the empty string). This hex value should be used as the input hexcode for get_FLAG_from_HEX(...), as described in the docstring. After passing through the SPECIAL_technique, you obtain the flag. Sorry I forgot source code solution...

brunner{7Urn5_0uT_th3Re_WasN7_4nY_SEcr3T5_4FtR_A1l_x)_Badum-tss}

Encrypted and Desperate

Writeup author: zBlxst

Xor encryption with a 16 bytes key. We have a png file, with a known 16 bytes (even more) header, so we can recover the key

Solution

from itertools import cycle
from pathlib import Path

TARGET_DIR = Path("./recipes/")


def encrypt(file, key):
    with open(file, "rb") as f:
        plaintext = f.read()

    ciphertext = bytes(a ^ b for a, b in zip(plaintext, cycle(key)))

    with open(f"{file}.dec", "wb") as f:
        f.write(ciphertext)

    print(f"Encrypted {file.name}")

png_header = b"\x89PNG\x0d\x0a\x1a\x0a" + b"\x00\x00\x00\x0dIHDR"
with open("recipes/1f.png.enc", "rb") as f:
    content = f.read(16)
    key = bytes(a ^ b for a, b in zip(png_header, content))
    print(key)

for file in TARGET_DIR.rglob("*.enc"):
        if file.is_file():
            encrypt(file, key)

brunner{mY_pr3c10u5_r3c1p35_U_f0und_7h3m}

Peppernuts

Writeup author: michalBB

I extracted the pepper e9d8 from nut_secure.py using a test hash for Test123! and the fact that pepper_size=16. Then, with the hashes, I guessed Brunner's password abcake and decrypted his recipe.

brunner{Maybe_we_could_mould_some_small_pieces_of_brunsviger_into_peppernut-shaped_treats?_:-D}

secret-brunner-recipe

Writeup author: michalBB

# -*- coding: utf-8 -*-
"""
solve_brunner_fixed.py — exploit for "Secret Brunner Recipe" (CTF crypto)
Fix: TenSEAL BFVVector often doesn't expose mul_plain/add_plain. Use operator
overloading instead: enc = enc * mask; enc = enc + add_plain.
"""

import sys
import time
import requests
import tenseal as ts

BASE = "https://secret-brunner-recipe-a17814770f301e73.challs.brunnerne.xyz"
PLAIN_MOD = 1032193
TARGET = "flødeskum"
ALPHABET = list("_ abcdefghijklmnopqrstuvwxyz{}")

session = requests.Session()


def fetch_bytes(url: str) -> bytes:
    r = session.get(url, timeout=20)
    r.raise_for_status()
    return r.content


def load_materials():
    pub_ctx_bytes = fetch_bytes(f"{BASE}/public")
    enc_bytes = fetch_bytes(f"{BASE}/secretrecipe")

    ctx = ts.context_from(pub_ctx_bytes)
    enc_vec = ts.bfv_vector_from(ctx, enc_bytes)

    try:
        length = enc_vec.size()
    except Exception:
        length = getattr(enc_vec, "size", None)
        if not isinstance(length, int):
            raise RuntimeError("Couldn't determine ciphertext vector length")

    return ctx, enc_bytes, length


def craft_probe(ctx, enc_bytes: bytes, length: int, pos: int, guess_char: str) -> bytes:
    # Choose window [s, s+8] so that pos is inside and it fits
    s = min(max(pos, 0), max(0, length - 9))
    j0 = pos - s

    enc = ts.bfv_vector_from(ctx, enc_bytes)

    # 1) Mask: keep only slot `pos`
    mask = [0] * length
    mask[pos] = 1
    enc = enc * mask  # plaintext elementwise multiply

    # 2) Add constants so that window becomes TARGET iff recipe[pos] == guess_char
    add_plain = [0] * length
    for k in range(9):
        idx = s + k
        if idx >= length:
            continue
        if k == j0:
            add_plain[idx] = (ord(TARGET[k]) - ord(guess_char)) % PLAIN_MOD
        else:
            add_plain[idx] = ord(TARGET[k]) % PLAIN_MOD

    enc = enc + add_plain  # plaintext elementwise add

    return enc.serialize()


def oracle(payload: bytes) -> bool:
    try:
        r = session.post(f"{BASE}/isTerrible", data=payload, timeout=20)
        return r.text.strip() == "True"
    except Exception:
        return False


def recover_secret():
    ctx, enc_bytes, length = load_materials()
    print(f"[+] Loaded materials. Ciphertext length: {length} slots")

    recovered = ["?"] * length

    for pos in range(length):
        found = None
        for ch in ALPHABET:
            payload = craft_probe(ctx, enc_bytes, length, pos, ch)
            if oracle(payload):
                recovered[pos] = ch
                found = ch
                break
        prefix = "".join(recovered[:pos + 1])
        print(f"[{pos+1:3d}/{length}] -> {found!r} | {prefix}")
        time.sleep(0.01)

    secret = "".join(recovered).rstrip("\\x00")
    print("\\n[+] Recovered secret:\\n" + secret)
    return secret


if __name__ == "__main__":
    if len(sys.argv) > 1:
        BASE = sys.argv[1].rstrip("/")
    recover_secret()

brunner{tbsp_of_brown_sugar}

pretzel

Writeup author: michalBB

Solution

# -*- coding: utf-8 -*-
# solve_pretzel.py
# Rozwiązuje zadanie "pretzel": odzyskuje brunner{...} z public.py + pretzel.csv

import math, random, csv
from typing import Dict, Tuple

# --- dane publiczne ---
from public import p_list, a_list, G_list, looks_done

# --- arytmetyka na (pseudo)krzywej jak w pretzel.py ---
def inv(x, p): return pow(x, p-2, p)

def add(P, Q, p, a):
    if P is None: return Q
    if Q is None: return P
    x1, y1 = P; x2, y2 = Q
    if x1 == x2 and (y1 + y2) % p == 0:
        return None
    if P == Q:
        slope = (3 * x1 * x1 + a) * inv((2 * y1) % p, p) % p
    else:
        slope = (y2 - y1) * inv((x2 - x1) % p, p) % p
    x3 = (slope * slope - x1 - x2) % p
    y3 = (slope * (x1 - x3) - y1) % p
    return (x3, y3)

def mul(k, P, p, a):
    R = None
    A = P
    while k:
        if k & 1: R = add(R, A, p, a)
        A = add(A, A, p, a)
        k >>= 1
    return R

# --- parametr u,t dla osobliwej krzywej y^2 = (x-1)^2 (x+2); NIE używamy do S, tylko do DLP ---
def sqrt_mod(a, p):
    # Tonelli–Shanks
    if a % p == 0: return 0
    if p % 4 == 3: return pow(a, (p+1)//4, p)
    # p-1 = q*2^s
    q = p-1; s=0
    while q % 2 == 0:
        q//=2; s+=1
    z = 2
    while pow(z, (p-1)//2, p) != p-1:
        z += 1
    c = pow(z, q, p)
    x = pow(a, (q+1)//2, p)
    t = pow(a, q, p)
    m = s
    while t != 1:
        i=1; t2i=(t*t)%p
        while t2i != 1:
            t2i=(t2i*t2i)%p
            i+=1
        b = pow(c, 1 << (m-i-1), p)
        x = (x*b) % p
        t = (t*b*b) % p
        c = (b*b) % p
        m = i
    return x

def t_of_point(P, p):
    x,y = P
    u = (y * inv((x-1) % p, p)) % p
    s = sqrt_mod(3, p)         # tangensy w węźle: ±sqrt(3)
    # t = (u - s) / (u + s)  -> mnożenie t odpowiada dodawaniu punktów
    return ((u - s) * inv((u + s) % p, p)) % p

# --- narzędzia liczbowe ---
def gcd(a,b):
    while b: a,b = b, a%b
    return a

def is_probable_prime(n, k=10):
    if n < 2: return False
    small = [2,3,5,7,11,13,17,19,23,29,31,37]
    for q in small:
        if n % q == 0: return n == q
    d = n-1; s=0
    while d % 2 == 0:
        d//=2; s+=1
    rng = random.Random(0xC0FFEE)
    for _ in range(k):
        a = rng.randrange(2, n-2)
        x = pow(a, d, n)
        if x in (1, n-1): continue
        for _ in range(s-1):
            x = (x*x) % n
            if x == n-1: break
        else:
            return False
    return True

def pollards_rho_int(n):
    if n % 2 == 0: return 2
    if n % 3 == 0: return 3
    rng = random.Random(1337)
    while True:
        c = rng.randrange(1, n-1)
        f = lambda x: (x*x + c) % n
        x = rng.randrange(2, n-1)
        y = x
        d = 1
        while d == 1:
            x = f(x); y = f(f(y))
            d = gcd(abs(x - y), n)
        if d != n:
            return d

def factor(n) -> Dict[int,int]:
    fac = {}
    def _f(n):
        if n == 1: return
        if is_probable_prime(n):
            fac[n] = fac.get(n,0) + 1
        else:
            d = pollards_rho_int(n)
            _f(d); _f(n//d)
    _f(n)
    return fac

def crt_pair(a1,m1,a2,m2):
    t = ((a2 - a1) * pow(m1, -1, m2)) % m2
    return (a1 + m1*t) % (m1*m2), m1*m2

def crt_all(congs):
    x, m = 0, 1
    for a,mod in congs:
        x, m = crt_pair(x, m, a, mod)
    return x % m, m

def bsgs(base, target, order, p):
    m = int(math.isqrt(order)) + 1
    table = {}
    cur = 1
    for j in range(m):
        if cur not in table:
            table[cur] = j
        cur = (cur * base) % p
    factor = pow(base, -m, p)
    gamma = target
    for i in range(m+1):
        if gamma in table:
            return (i*m + table[gamma]) % order
        gamma = (gamma * factor) % p
    return None

def pollard_rho_dlp_subgroup(p, g, h, q, tries=24, max_steps=150_000_000):
    # Rozwiązuje g^x = h w podgrupie rzędu q
    def step(a,b,X):
        s = X & 3
        if s == 0:
            return (a+1)%q, b, (X*g)%p
        elif s == 1:
            return a, (b+1)%q, (X*h)%p
        elif s == 2:
            return (a*2)%q, (b*2)%q, (X*X)%p
        else:
            return (a+1)%q, (b+1)%q, (X*g*h)%p

    for seed in range(tries):
        rng = random.Random(424242 + seed)
        a = rng.randrange(0, q); b = rng.randrange(0, q)
        X = (pow(g, a, p) * pow(h, b, p)) % p
        a2, b2, X2 = a, b, X
        for _ in range(1, max_steps+1):
            a,b,X   = step(a,b,X)
            a2,b2,X2= step(*step(a2,b2,X2))
            if X == X2:
                r = (a - a2) % q
                s = (b2 - b) % q
                if s == 0:
                    break
                x = (r * pow(s, -1, q)) % q
                if pow(g, x, p) == h:
                    return x
                # Jeśli kolizja "fałszywa", też często jest dobrym x (ale weryfikujemy wyżej)
                return x
    return None

# --- właściwy Pohlig–Hellman: najpierw ord(g), potem stały g_q ---
def pohlig_hellman_fpstar(p, g, h) -> int:
    n = p - 1
    fac_n = factor(n)

    # RZĄD rzeczywisty g (usuwamy czynniki, które nie dzielą ord(g))
    ord_g = n
    for q,e in fac_n.items():
        while ord_g % q == 0 and pow(g, ord_g // q, p) == 1:
            ord_g //= q

    fac_ord = factor(ord_g)
    parts = []
    for q, e in fac_ord.items():
        # stały generator podgrupy rzędu q
        gq = pow(g, ord_g // q, p)
        if gq == 1 or pow(gq, q, p) != 1:
            raise RuntimeError("Nie udało się uzyskać elementu rzędu q")

        x_mod, mod = 0, 1
        for j in range(e):
            c = (h * pow(g, -x_mod, p)) % p
            cj = pow(c, ord_g // (q**(j+1)), p)

            if q < 1_000_000:
                dj = bsgs(gq, cj, q, p)
            else:
                dj = pollard_rho_dlp_subgroup(p, gq, cj, q)
            if dj is None:
                raise RuntimeError("DLP w podgrupie rzędu q nie powiodło się")

            x_mod = (x_mod + dj * (q**j)) % (q**(j+1))
            mod   = q**(j+1)

        parts.append((x_mod, q**e))

    x, _ = crt_all(parts)
    return x % ord_g

# --- IO pretzel.csv ---
def load_csv(path="pretzel.csv"):
    rows = []
    with open(path, newline="") as f:
        r = csv.DictReader(f)
        for row in r:
            rows.append({
                "idx": int(row["curve_index"]),
                "Rx": int(row["Rx"]), "Ry": int(row["Ry"]),
                "Qx": int(row["Qx"]), "Qy": int(row["Qy"]),
            })
    rows.sort(key=lambda r: r["idx"])
    return rows

# --- KDF + AES-GCM ---
from cryptography.hazmat.primitives.kdf.hkdf import HKDF
from cryptography.hazmat.primitives.hashes import SHA256
from cryptography.hazmat.primitives.ciphers.aead import AESGCM

def derive_key(dough: bytes) -> bytes:
    hk = HKDF(algorithm=SHA256(), length=32,
              salt=b"pretzelsalt-sprinkle_for_the_win",
              info=b"pretzelbaking")
    return hk.derive(dough)

def main():
    rows = load_csv()
    (p1,a1,G1), (p2,a2,G2) = (p_list[0],a_list[0],G_list[0]), (p_list[1],a_list[1],G_list[1])
    R1 = (rows[0]["Rx"], rows[0]["Ry"]); Q1 = (rows[0]["Qx"], rows[0]["Qy"])
    R2 = (rows[1]["Rx"], rows[1]["Ry"]); Q2 = (rows[1]["Qx"], rows[1]["Qy"])

    # DLP w F_{p2}^*: t(Q) = t(G)^d
    tG2 = t_of_point(G2, p2)
    tQ2 = t_of_point(Q2, p2)
    d = pohlig_hellman_fpstar(p2, tG2, tQ2)
    # sanity
    assert pow(tG2, d, p2) == tQ2, "weryfikacja d nie przeszła"

    # S = d * R (bo kQ = dR) – liczymy dokładnie tą samą add/mul co w zadaniu
    S1 = mul(d, R1, p1, a1)
    S2 = mul(d, R2, p2, a2)

    # 'dough' jak w pretzel.py
    dough = b""
    for S in (S1, S2):
        Sx = S[0]
        dough += Sx.to_bytes((Sx.bit_length()+7)//8, "big") if Sx else b""

    key = derive_key(dough)
    nonce = b"pretzelnonce"
    pt = AESGCM(key).decrypt(nonce, bytes.fromhex(looks_done), None).decode()
    print("FLAG:", f"brunner{{{pt}}}")

if __name__ == "__main__":
    main()

brunner{1F_y0u_9iVe_4n_El1IpTiC_cUrve_4_SPl17_N0dE,_A5_a_tRaNsV3rSE_5eLf-In7Er5ectiOn,_4nD_A_6ad_P,i7_6EComeS_Ins3cUrE:)}

pi-crypt

Writeup author: ppp45

I slightly edited the code from original file to make it more descriptive

assert len(ALPHA) == 100 and len(PI) == 1000


def cipher(pt, key, decrypt=False, starting_x=None):
    shift_log = []
    ct = ""

    # equivalent to consecutive x_incr
    key_to_indexes = [ALPHA.index(char) for char in key]

    # x is effectively MOD 1000
    if starting_x is not None:
        x = starting_x
    else:
        x = sum(key_to_indexes)

    print(f"{x % 1000 = }")

    t = 0

    for char in pt:
        #  PI digit based on x
        digit_1 = int(PI[x % len(PI)])
        #  alpha-index of next key char (cycling)
        x_incr = ALPHA.index(key[t % len(key)])
        x += x_incr
        t += 1

        # same logic repeated second time
        digit_2 = int(PI[x % len(PI)])
        x_incr = ALPHA.index(key[t % len(key)])
        x += x_incr
        t += 1

        # two consecutive key chars result in single pt char shift
        shift = 10 * digit_1 + digit_2

        shift_log.append(shift)

        ct += ALPHA[(ALPHA.index(char) + (-shift if decrypt else shift)) % len(ALPHA)]

    print(f"{shift_log = }")
    return ct


N = len(PI)
assert N == 1000

We know the first 8 characters and last 1 character of the key (flag).

assert all(c in ALPHA for c in pt + key) and key[:8] + key[-1] == "brunner"

Because starting_x is modulo 1000, there aren't that many possibilities. We use key=PREFIX and print all possibilities. Only one of them (765) returns a plaintext starting with "clean" 4 letters: Blue.

We call this number a KEY_WEIGHT and use its multiples modulo 1000 to recover key length.

Each ct/pt character is affected by two consecutive characters of the key. We divide ciphertext into blocks of the size equal to the potential key length. That corresponds to the using full key two times - we don't know if the key has odd or even length but its double is always even.We call this number a KEY_WEIGHT and use its multiples modulo 1000 to recover key length.

def decrypt(inp, key, starting_x):
    out = ""
    shift_sum = 0

    x = starting_x

    t = 0

    for char in inp:
        #  PI digit based on x
        a = int(PI[x % len(PI)])
        #  alpha-index of next key char (cycling)
        x_incr = ALPHA.index(key[t % len(key)])
        x += x_incr
        t += 1

        # same logic repeated second time
        b = int(PI[x % len(PI)])
        x_incr = ALPHA.index(key[t % len(key)])
        x += x_incr
        t += 1

        # two consecutive key chars result in single pt char shift
        shift = 10 * a + b

        shift_sum += shift

        out += ALPHA[(ALPHA.index(char) - shift) % len(ALPHA)]

    return out


N = len(PI)
assert N == 1000

PREFIX = "brunner{"
SUFFIX = "}"
KEY_WEIGHT = 765

CT_FILE = "REAL_CT.txt"

with open(CT_FILE, encoding="utf-8") as f:
    ct = f.read()


relevant_chars = len(PREFIX) // 2


for skipped in range(10):
    # whole key two times to ensure even number of chars
    starting_x = (KEY_WEIGHT * (1 + 2 * skipped)) % N

    print(f"\n{skipped = }\n{"-" * 64}")

    for inner_flag_size in range(1, 100):
        key_size = len(PREFIX) + inner_flag_size + len(SUFFIX)
        ignored = key_size * skipped
        ct_part = ct[ignored:]

        pt_part = decrypt(ct_part, PREFIX, starting_x=starting_x)[:relevant_chars]

        print(f"{inner_flag_size:02}    {pt_part}")

It's easy to see that the correct inner flag length is 66:

63    l�9K
64    >O5e
65    fK[`
66    berr
67    v`~i
68    Nr}
69    8iP$

63    fr/j
64    geu<
65    ;]%y
66    ste,
67    <�xr
68    CmW,
69    (�O&

As the flag itself says, it would have been harder with a key of even length. To get more blocks (and their starting characters to assess) we split each block of size 75 into blocks of 37 and 38 chars. The key wraps around, so for the first block we use brunner{ and for the second one - }brunner{. By adjusting starting_x properly (subtracting and adding the "weight" of {) we are able to correctly decrypt initial characters of both type of blocks.

Finally, we repeatedly use all possible 10000 character pairs to find the next two characters of the flag.

assert len(ALPHA) == 100

N = len(PI)
assert N == 1000

KEY_PREFIX = "brunner{"
KEY_SUFFIX = "}"

KEY_WEIGHT = 765
KEY_SIZE = 75

CT_FILE = "REAL_CT.txt"


# TEST
# KEY_WEIGHT = 860
# CT_FILE = "TEST_CT.txt"
# TEST


def calculate_weight(key):
    key_to_indexes = [ALPHA.index(char) for char in key]
    return sum(key_to_indexes) % N


def decrypt(inp, key, starting_x):
    out = ""
    shift_sum = 0

    x = starting_x

    t = 0

    for char in inp:
        #  PI digit based on x
        digit_1 = int(PI[x % len(PI)])
        #  alpha-index of next key char (cycling)
        x_incr = ALPHA.index(key[t % len(key)])
        x += x_incr
        t += 1

        # same logic repeated second time
        digit_2 = int(PI[x % len(PI)])
        x_incr = ALPHA.index(key[t % len(key)])
        x += x_incr
        t += 1

        # two consecutive key chars result in single pt char shift
        shift = 10 * digit_1 + digit_2

        shift_sum += shift

        out += ALPHA[(ALPHA.index(char) - shift) % len(ALPHA)]

    return out




# decrypt blocks individually so the beginning is correct even if key weight is wrong
def decrypt_blocks(ct, key, relevant_chars):
    # one block per one odd-size key run
    assert KEY_SIZE % 2 == 1

    SUFFIX_WEIGHT = calculate_weight(KEY_SUFFIX)

    ct_blocks = []
    start = 0

    for idx in range(2 * math.ceil(len(ct) / KEY_SIZE)):
        size = KEY_SIZE // 2
        if idx % 2 == 1:
            size += 1
        end = start + size
        ct_blocks.append(ct[start:end])
        start = end

    pt_blocks = []
    starting_x = KEY_WEIGHT

    for idx, ct in enumerate(ct_blocks):
        if idx % 2 == 0:
            temp_key = key
            temp_relevant_chars = relevant_chars
        else:
            temp_key = KEY_SUFFIX + key
            temp_relevant_chars = relevant_chars + 1

        pt = decrypt(ct, temp_key, starting_x)
        pt_blocks.append(pt[:temp_relevant_chars])

        if idx % 2 == 0:
            starting_x += KEY_WEIGHT - SUFFIX_WEIGHT
        else:
            starting_x += KEY_WEIGHT + SUFFIX_WEIGHT
        starting_x %= N

    return tuple(pt_blocks)

with open(CT_FILE, encoding="utf-8") as f:
    ct = f.read()


RECOVERED_INNER_KEY = "1t_W0ulD"


all_results = {}

for char_1 in ALPHA:
    for char_2 in ALPHA:
        key = KEY_PREFIX + RECOVERED_INNER_KEY + char_1 + char_2
        assert len(key) % 2 == 0
        relevant_chars = len(key) // 2

        pt_blocks = decrypt_blocks(ct, key, relevant_chars)
        all_results[key] = pt_blocks

unique_results = set(all_results.values())


def is_good(res):
    required = [
        "",
        "",
        "",
        "",
        "",
    ]

    return all(e in res for e in required if e)


filtered_results = {}

for key, res in all_results.items():
    if is_good(res):
        filtered_results.setdefault(res, []).append(key)

print(f"{len(unique_results) = }")
print(f"{len(filtered_results) = }")

with open("results.txt", "w", encoding="utf-8") as f:
    for res, keys in filtered_results.items():
        f.write(f"{keys = }\n{"-" * 64}\n")
        f.write("\n".join(res) + "\n\n\n")

We narrow down the number of results by adding predicted correct texts to the required list, e.g. "Blueberry", "consists o" and "sweetness" in that case.

Blueberr5
oved by bQ
berries X
 a deep bn
ste, whiW
 goods - .
ries areÆ
juicy wit,
 A tradip
consists ø
th a cruw
 (which c!
 crumb).Æ
 use abouD
-3 tableq
oons of c+
ttle leml
 twist. B@
 in antio
 24% of tQ
 makes tg
so a bit æ
 them wiv
ood pie sS
sweetnest

brunner{1t_W0ulD_H4v3_6een_H@rDeR_Thou9h(!),w1th_Å_k3y_Øf_Ev3n-LÆNgth.`:-7}

Bonus

You can get binaries from github