team-logo
Published on

BITSCTF 2025 - CRYPTO challenges

Authors

Introduction

We solved 3 out of 6 tasks. But one was first blood.

Table of contents

Baby Crypto

Baby Crypto

Writeup author: ppp45

We know n, e and ct (encrypted flag). We can decrypt any chosen ciphertext except ct.

Since:

decrypt(k*ct) = (k*ct)^d = k^d * ct^d = k^d * pt mod n

we need to choose k for which we know k^d mod n

Because (x^e)^d = x mod n, we calculate k = 2^e mod n (in other words we encrypt number 2).

We use the oracle to decrypt k * ct and receive the plaintext (flag) multiplied by 2.

Flag: BITSCTF{r54_0r4acl3_h4s_g0t_t0_b3_0n3_0f_7h3_3as13st_crypt0_1n_my_0p1n10n_74b15203}

The most wanted lagomorph

lagomorph
We got here first blood. blood

Writeup author: umz

First, decrypted using ROT-8000, and the resulting content contained characters from i to m, which clearly doesn't match hex format. So, tried iterating through all possible values using characters a-f. After testing, found that when i=e, j=d, k=c, l=b, and m=a, the result was valid. Additionally, i=e, j=d, k=c, l=f, and m=a also worked. Given the clue "No More Bunny Business", thought of rabbit encryption and used the rabbit name "dennis" as the password to decrypt and finally obtain the flag. 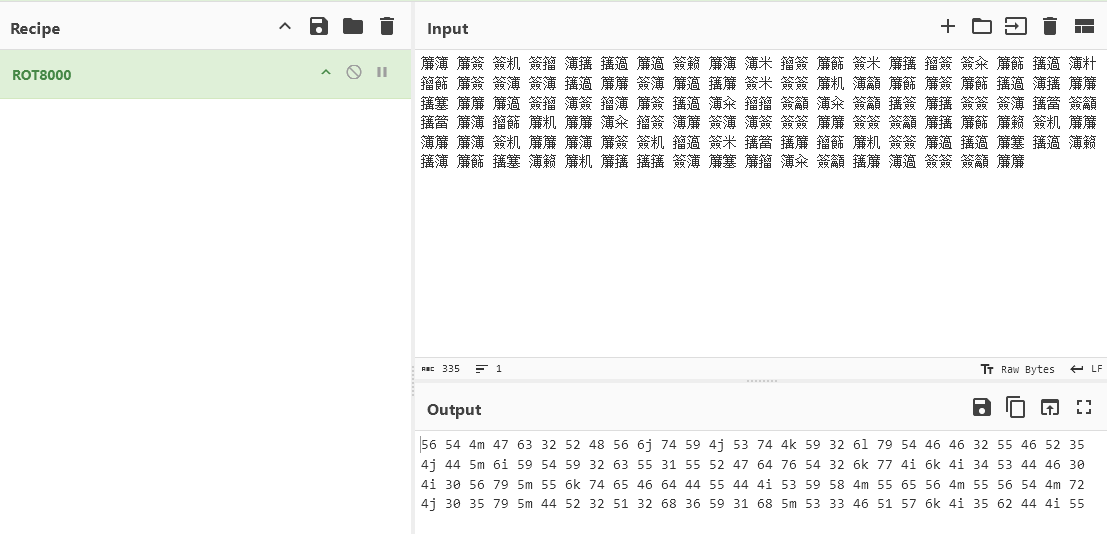rot-8000
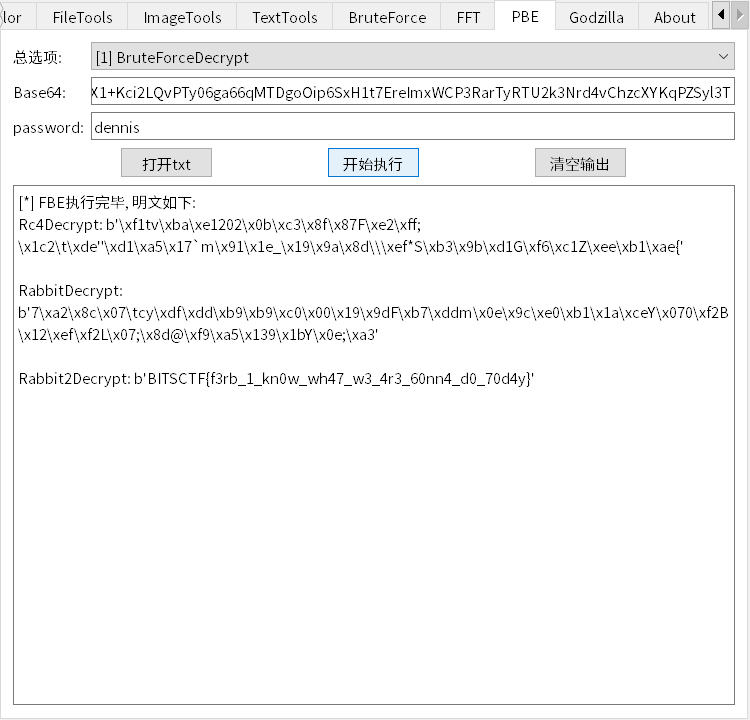
decrypt-bunny U2FsdGVkX1+Kci2LQvPTy06ga66qMTDgoOip6SxH1t7EreImxWCP3RarTyRTU2k3Nrd4vChzcXYKqPZSyl3T

https://www.browserling.com/tools/rabbit-decrypt

Flag: BITSCTF{f3rb_1_kn0w_wh47_w3_4r3_60nn4_d0_70d4y}

Noob RSA returns

Noob RSA Returns Writeup author: ppp45

We are given a Python script and its output:

from Crypto.Util.number import getPrime, bytes_to_long

def GenerateKeys(p, q):
    e = 65537
    n = p * q
    phi = (p-1)*(q-1)
    d = pow(e, -1, phi)
    C = 0xbaaaaaad
    D = 0xdeadbeef
    A= 0xbaadf00d
    K = (A*p**2 - C*p + D)*d
    return (e, n, K)

def Encrypt():
    flag = b"REDACTED" # HEHEHEHEHE
    p = getPrime(512)
    q = getPrime(512)
    e, n, K = GenerateKeys(p, q)
    pt = bytes_to_long(flag)
    ct = pow(pt, e, n)

    print(f"e = {e}")
    print(f"n = {n}")
    print(f"ct = {ct}")
    print(f"K = {K}")

Encrypt()

e = 65537
n = 94391578028846794543970306963076155289398888845132329034244336898352288130614402434536624297683695128972774452047972797577299176726976054101512298009248486464357336027594075427866979990479026404794249095503495046303993475122649145761379383861274918580282133794104162177538259963029805672413580517485119968223
ct = 39104570513649572073989733086496155533723794051858605899505397827989625611665929344072330992965609070817627613891751881019486310635360263164859429539044097039969287153948226763672953863052936937079161030077852648023719781006057880499973169570114083902285555659303311508836688226455433255342509705736365222119
K = 20846957286553798859449981607534380028938425515469447720112802165918184044375264023823946177012518880630631981155207307372567493851397122661053548491580627249805353321445391571601385814438186661146844697737274273249806871709168307518276727937806212329164651501381607714573451433576078813716191884613278097774416977870414769368668977000867137595804897175325233583378535207450965916514442776136840826269286229146556626874736082105623962789881101475873449157946816513513532838149452759771630220014344325387486921028690085783785067988074331005737389865053848981113695310344572311901555735038842261745556925398852334383830822697851

During CTF I came up with a rather inefficient solution but decided to stick with it and focus on other challenges.

If we knew z:

z = (e * d - 1) // phi

we could eliminate other variables and a univariate equation involving single variable p.

z is an integer not greater than e (I didn't try to prove it but calculated it multiple times for different random p and q).

The following script contains equations (assertions) and using the last one we can calculate p using sympy (z3 turned out to be slower in that case).

from Crypto.Util.number import getPrime

A = 0xBAADF00D
B = 0xBAAAAAAD
C = 0xDEADBEEF
e = 65537


def GenerateKeys(p, q):
    n = p * q
    phi = (p - 1) * (q - 1)
    d = pow(e, -1, phi)

    K = (A * p**2 - B * p + C) * d
    return (e, n, K)


p = getPrime(512)
q = getPrime(512)
e, n, K = GenerateKeys(p, q)

# ------------------------------

phi = (p - 1) * (q - 1)
d = pow(e, -1, phi)
z = (e * d - 1) // phi
print(f"{z = }")

# ------------------------------


# 1
assert phi == n + 1 - (p + n // p)

# 2
assert d == (z * phi + 1) // e

# 3
assert d == (z * (n + 1 - (p + n // p)) + 1) // e

# 4
assert d == K // ((A * p**2 - B * p + C))

# 5
assert K // ((A * p**2 - B * p + C)) == (z * (1 + n - p - n // p) + 1) // e

# 6
assert K * e == ((A * p**2 - B * p + C)) * (z * (1 + n - p - n // p) + 1)

Basic solver concept:

from sympy import symbols, solve, Eq, isprime


START = 1
END = e

p = symbols("p", integer=True)

for z in range(START, END + 1):
    print(f"{z = }")
    equation = Eq(K / ((A * p**2 - B * p + C)), (z * (n + 1 - (p + n / p)) + 1) / e)

    solutions = solve(equation, p)

    for sol in solutions:
        if sol.is_integer:
            print(f"{int(sol) = }")
            exit()

For z = 42677 we recover p which allows us to calculate private key d and decrypt the flag.

p = 10406216443192169173533723167461845081683996237790486467542778667477564930803546070928131853072839096935544813786122096301171127932695303325352097678393621

q = n // p
assert n == p * q

d = pow(e, -1, (p - 1) * (q - 1))
pt = pow(ct, d, n)

print(pt.to_bytes(99))

Flag: BITSCTF{I_H0P3_Y0UR3_H4V1NG_FUN_S0_F4R_EHEHEHEHEHO_93A5B675}